Книга "Математические начала теории ограничений" является первой из серии книг, объединённых наименованием "Бизнес-процессы компании "Any" и посвящена созданию общего компактного математического описания сходных понятий разных методик управления и не только управления (таких как: "мини-задача", "принцип минимума", "узкое место", "наименьшее действие", "повышение идеальности" и др.).

Она имеет целью создать простой формальный инструмент для превращения сложных предпринимательских (как коммерческих, так и производственных) задач в простые. С тем, чтобы как Предприниматель, так и Изобретатель, могли не просто достигать больших результатов, но делали это сокращая усилия и затраты.

НЕ ЗАБЛУДИТЕСЬ В ВЫЧИСЛЕНИЯХ

Задача 0.
Почти олимпиадная - для технологов и менеджеров по управлению производством

Условие: Все одинаковые изделия были изготовлены за 99 минут.

Вопрос-1: "Сколько их было, если 3 изделия изготовлены за 17 минут, а разность между временем изготовления 7-ми и 2-х составила 20 минут?"

Вопрос-2: "Какова продолжительность самой долгой операции этого процесса?"

Вопрос-3: "Сколько времени изготавливалось одно изделие, например, первое?"

Вопрос-4: "Сколько минут потеряно?"

Вопрос-5: "Сколько времени простояло в очередях на обработки предпоследнее изделие из изготовленных?"

Попробуйте ответить на каждый из вопросов прежде, чем читать дальше. Если не справитесь, попробуйте решить следующую задачу, а потом вернитесь к этой.

Задача 1. Стартовая

1 изделие, проходя ряд последовательных операций (A, B, C, etc.), производится за T минут = (T1 + T2 + T3 + ...Tn) - Рис. 1. За сколько минут будет произведено N тех же изделий?

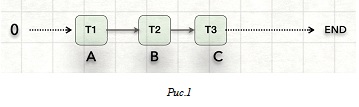
• Одинаковые изделия;
• Та же последовательность тех же операций;
• То же оборудование;
• Те же люди.

Конечно, ответ: N x T - неверный. Время всех операций суммируется лишь тогда, когда производится всего 1 изделие - то есть, когда нет случая, чтобы какие-либо операции происходили одновременно.

Например, время изготовления первого изделия на Рис. 2 ниже: 2 + 4 + 3 = 9 нетто-минут. Но на 2 изделия израсходуется 13 нетто-минут, а не 18, как может стереотипно показаться.

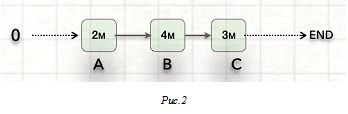
Потому что когда операция B ещё "трудится" над первым изделием, в это же время операция A "трудится" уже над вторым. Если условия задачи 0 Вам показались противоречивыми, то это именно потому, что данный факт не был принят Вами во внимание.

Что ж, попробуйте, прежде чем читать дальше, решить задачу 1, а затем задачу 0 (после верного решения задачи 1 это будет несложно).

Решаем задачу 1

Как сказано выше, при производстве одного изделия (например, первого) нет одновременности. Следовательно, время изготовления первого изделия равно простой сумме времён операций, участвовавших в его изготовлении. (А в сетевом случае - сумме времён операций, лежащих на самой долгой траектории процесса, которую называют обычно "критическим путём".)

• Время производства первого изделия или единственного назовём: Tf (Tfirst). Нетрудно заметить, что, поскольку "первый не дожидается" - это также и то время, когда каждое изделие обрабатывается.
• Время производства N изделий назовём: Tn

Тогда Tn = Tf + (Всё остальное)

Всё остальное = Остальные изделия (то есть, (N - 1)) * (Какое-то время).

Тогда Tn = Tf + (N - 1)*(Какое-то время)

Очевидно, что скорость движения всего потока не будет выше скорости обработки в "узком месте". Следовательно,"какое-то время" - это время самой долгой операции процесса. Назовём её Tl (Tlongest).

Тогда Tn = Tf + Tl * (N-1) - эталонное время Tn процесса для производства N изделий. Которое, как видно, при любой траектории процесса определяется двумя компактными параметрами:

• Временем производства единственного изделия или первого Tf и
• Временем, затраченным на самую долгую операцию этого процесса Tl.

Без сомнения перед нами формула арифметической прогрессии, где время самой долгой операции Tl является "шагом".

Это значит, что каждое следующее изделие, начиная со второго, будет выходить через Tl после предшествующего. Например, в случае, показанном на Рис.2 - через каждые 4 минуты.

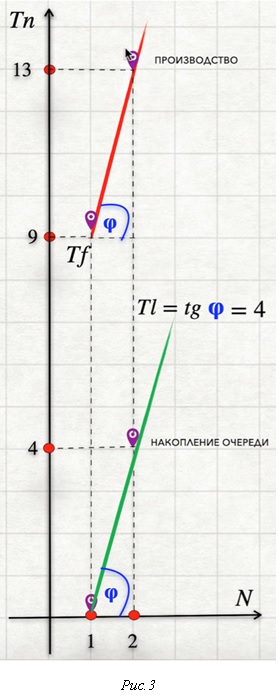
Скорость роста функции (производная по N) здесь равна Tl и это тоже означает, что производительность процесса определяется "узким местом", и им же определяется скорость роста очереди на обработку.

Общее время Tn, как видно из формулы, состоит из времени Tf, когда единица изделия обрабатывается, и времени, когда она не обрабатывается: Tl * (N - 1), что и есть время ожидания N-ой единицы в очереди, а скорость прироста этой очереди (производная по N) равна Tl.

Последнюю фразу всякий производственник может назвать "Введением в "незавершёнку" - та же формула, где Tf = 0.

Графики на Рис.3 построены для примера, разобранного в задаче 1 (см. Рис.2). Красная линия показывает график производства, а зелёная линия показывает накопление очереди.

Автор настоящего текста, Сергей Сычёв, предположительно первым изложил математически данным образом многочисленные "аналоговые" описания "узких мест" в разных методиках управления. Он указал на следующее:

• Время, необходимое для изготовления любого количества изделий, также и время, которое проводит единица изделия в очередях в ожидании обработок, определяется арифметической прогрессией с шагом, равным времени наиболее продолжительной операции процесса.
• Этот "шаг" (скорость роста функции, коэффициент линейной функции), очевидно, является производной времени изготовления по числу изделий. Это и значит: "узкое место определяет скорость процесса".
• Это правило не зависит от "топологии" технологической сети, не зависит от количества "цепочек» или иных участков сложного процесса и не зависит от траекторий движения изготовляемых изделий.

В теории ограничений Э. Голдратта вместо приводимой здесь математики используется слово "барабан". Воздавая должное этому неординарному профессионалу, тем не менее укажем, что аналогии и метафоры, проясняя (иногда, впрочем, и запутывая) суть предмета, в реальном деле даже нашу простую задачу 1 решить не позволяют, не говоря уже о задачах более сложных. В известном смысле от начала главы и до этого места изложено всё методическое содержание его книги "Цель-1" (что не умаляет достоинств автора книги).

Теперь несложно решить и Задачу 0

Итак, все одинаковые изделия были изготовлены за 99 минут.

Вопрос-1: "Сколько их было, если 3 изделия изготовлены за 17 минут, а разность между временем изготовления 7-ми и 2-х составила 20 минут?"

Вопрос-2: "Какова продолжительность самой долгой операции этого процесса?"

Вопрос-3: "Сколько времени изготавливалось одно изделие, например, первое?"

Вопрос-4: "Сколько минут потеряно?"

Вопрос-5: "Сколько времени простояло в очередях на обработки предпоследнее изделие из изготовленных?"

Система уравнений составляется достаточно просто, просто и решается - три уравнения, три неизвестных:

• Tf + Tl x (N - 1) = 99
• Tf + 2Tl = 17
• (Tf + 6Tl) - (Tf + Tl) = 20

За 99 минут было изготовлено 23 изделия (хотя корень 23,5, ясно, что, по факту, было сделано 23). Продолжительность самой долгой операции = 4 минуты. Первое изделие изготавливалось 9 минут. Потеряно 2 минуты, поскольку 23 изделия можно было произвести за 97 минут: Tf + Tl x (N - 1) = 9 + 4 * 22 = 97. Предпоследнее, 22-е изделие, простояло в очередях на обработки 84 минуты = 4 * 21.

КАК НАСЧЁТ СЛОЖНОГО ПРОЦЕССА?

Задача 2. "Некритическая"

Выше мы рассмотрели простую ситуацию с несколькими последовательными операциями, "лежащими" на одной линии процесса. Но как рассчитать длительность эталонного процесса для производства N изделий в сложной технологической сети?

Например, посмотрите на Рис. 4 (ниже) и ответьте на вопрос: "За сколько времени здесь будут изготовлены 100 одинаковых изделий?"

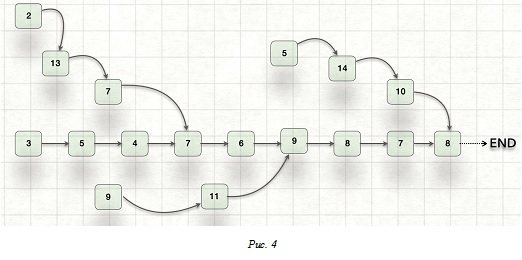
Здесь, как и выше, числа в квадратах - это минуты (продолжительность соответствующей операции), стрелки показывают направление движения потоков.

Попробуйте решить задачу прежде, чем читать дальше. 99 человек из 100 ошибаются, несмотря на знание "критического пути" и многого другого.

Очевидно, чтобы решить задачу 2, необходимо найти на схеме самую долгую "ветку" при 100 изделиях и посчитать её продолжительность. Почти каждый, кто пробует решить задачу, почему-то выбирает "красную "ветку" в качестве самой долгой (Рис. 5), а некоторые вдобавок умножают её продолжительность на 100 и это, разумеется, ужасно. А каков Ваш выбор?

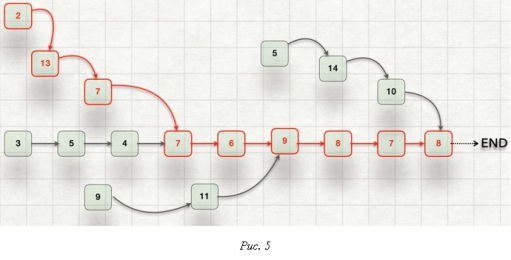
Те, кто выбрал "красную ветку", говорят:

"Я выбрал её, поскольку это "критический путь", он самый долгий и связан со всеми прочими "ветками". Его продолжительность 67 минут. Продолжительность остальных меньше".

Вы согласны с этим аргументом? Если "Да", ответьте, пожалуйста, на вопрос: "Почему Вы думаете о производстве одного изделия, когда в условии указано 100? Вы точно не сбились со счёта?"

Чтобы вновь не заблудиться в вычислениях глядя на Рис. 5, перечитайте также и условия задачи 1, прежде чем считать и читать дальше.

В выбранной Вами "красной ветке" 1 (одно) изделие проходит ряд последовательных операций за 67 минут. За сколько минут по этой же "ветке" пройдут 100 таких изделий?

• Одинаковые изделия;
• Та же последовательность тех же операций;
• То же оборудование;
• Те же люди.

Конечно ответ 67 x 100 - неверный! Так что если Вы выбрали "красную ветку", делайте вторую попытку.

В ПОИСКАХ РЕШЕНИЯ ЗАДАЧИ 2

Нам нужно найти на схеме самую долгую "ветку" при 100 изделиях, а не при одном, и посчитать её продолжительность. Как мы можем сделать это?

Шаг 1. Укажите на самую долгую операцию ("узкое место") всего процесса.

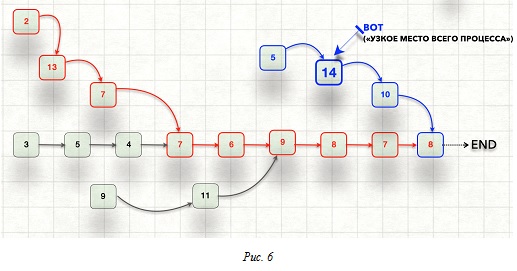
Шаг 2: Подсчитайте (для случая "100 изделий") производительность "ветки», содержащей самую долгую операцию всего процесса. Мы уже знаем, по какой формуле это считать.

T100 = Tf + Tl * (100 - 1) = 37 + 14 * 99 = 1423 (Вот корректный ответ на задачу 2)

Если Вы сомневаетесь, сравните результаты "синей ветки" и "красной ветки":

T100 = Tf + Tl * (100 - 1) = 37 + 14 * 99 = 1423

T100 = Tf + Tl * (100 - 1) = 67 + 13 * 99 = 1354 (и уж, конечно, не 6700)

1423 > 1354 Почему Вы назвали красную "критическим путём"?

ЗАДАЧА 2. ОЧЕВИДНОЕ ПОЯСНЕНИЕ ОТВЕТА

Функция: Tf + Tl * (N - 1) растёт от увеличения N, а не Tf. Tf и Tl - константы, переменная - N. Следовательно, чем больше количество элементов N в общем потоке, тем быстрее (нежели в других"ветках") замедляется движение потока в "ветке", имеющей "узкое место".

Пример-аналог: дорога с узким местом, когда по ней едет одна машина и много машин (одна и та же дорога).

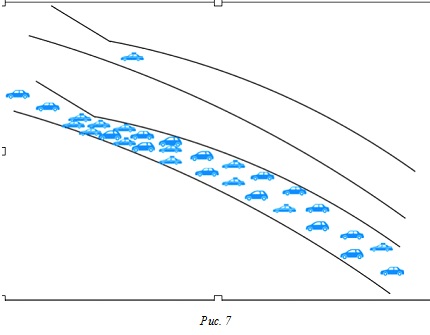
Где-то рядом (на картинке не видно) есть ещё объездная дорога - она длиннее, но шире. То, какой путь является самым долгим, больше зависит от времени преодоления узкого места Tl (что связано с числом машин N, приезжающих к узкому месту в единицу времени), чем от скорости одной машины, проталкивающейся сквозь более плотную среду.

Когда машина одна, то и "пробки" нет, и путь по объездной дороге получается дольше. Иное дело, когда машин много - тогда и по длинной дороге доедешь быстрее.

Пьер Ферма ещё в 1662 году показал, что даже луч света движется через разные среды не по кратчайшему пути, а по такому, чтобы суммарное время в пути сквозь эти среды было минимальным. Он преломляется под соответствующим углами, но этот ломаный путь (который геометрически длиннее прямого) - самый быстрый из возможных.

К примеру с авто мы ещё раз обратимся позже. А сейчас вернёмся к задаче 2.

ЗАДАЧА 2. ДОРОГИ, КОТОРЫЕ МЫ ВЫБИРАЕМ

Критическая ошибка самой концепции "критического пути" заключается в том, что во всяком примере "критическим" назван самый долгий путь производства единицы, а не потока. Одного изделия, а не N изделий. Но ведь это лишь частный случай более общего закона - то есть, случай когда (N - 1) = 0.

Метод "критического пути" предписывает нарушить фундаментальный естественно-научный принцип наименьшего действия, который реализуется в реальности - разумеется это невозможно: мы видим, что "критические пути" (скорее всего, мы прекратим использовать этот термин) меняются в зависимости от N (см. Таблицы на Рис.8), даже если одинаковые изделия производятся в одном потоке на одном и том же оборудовании одними и теми же людьми. Подобно тому как меняются критерии выбора дороги в зависимости от числа машин в узком месте, подобно тому как меняется угол преломления света при изменении плотности среды (отношения скоростей распространения света в разных средах и есть показатель преломления).

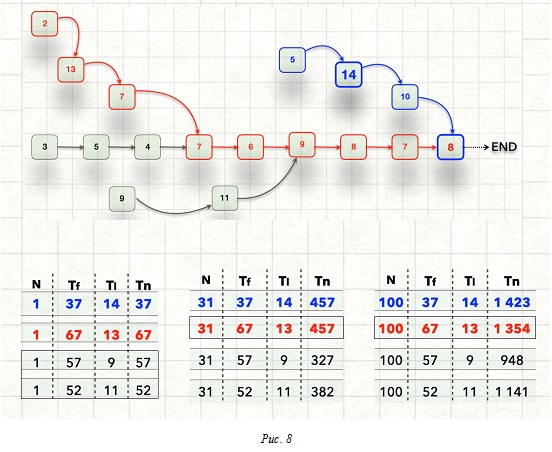
В нашем случае сначала (при изготовлении первого изделия) "критической" была "красная ветка", а начиная с 32-го изделия - "синяя".

Возразят, что "критический путь" как раз используется для проектных заданий - когда группа людей работает над одним сложным проектом, а не над потоком однотипных задач и в этом, якобы, отличие "проектных заданий" от "операционной деятельности".

Но нет никаких оснований не считать "проект" потоком задач (неважно разные они или однотипные), проходящих через людей, передающих далее результаты своих решений, которые собираются "на выходе" из процесса в одно "изделие/проект". Тогда очевидно, что, т.н. "критический путь проекта" (хоть бы проект был единственным) станет меняться каждый день, а то и чаще - как только любой исполнитель "залипнет" со своим заданием, превратившись в "узкое место" и создав новую "пробку", причём совсем необязательно на самой длинной "ветке". Какой тогда от него толк (не от исполнителя, а от "критического пути")?

Сверх того во множестве действующих проектных организаций обычно во всякий день выполняется более одного заказа в период времени - так что один человек в своё рабочее время может переключаться между разными (по сложности, продолжительности и т.д.) задачами. И если в проектах участвуют разные по качеству люди, то в реальности никакого "критического пути" как параметра оптимизации работ, вовсе не существует - так что, в худшем случае, "процессы" распадаются на некоторое количество "натуральных хозяйств" и деградируют, а в лучшем - участники процесса начинают работать "спринтами", имея лишь примерный общий план.

Мы сейчас не будем отвлекаться на это и продолжим наш "некритический путь". Но, вероятно, само понятие "критического пути" в менеджменте действительно становится лишним.

В любом случае обратите внимание: для того, чтобы корректно решить задачу 2 нам ведь, на самом деле, вовсе и не требуется рисовать никаких сетевых графиков и диаграмм PERT, верно?

ЗАДАЧА 3. ОШИБКА ИЗОБРЕТАТЕЛЯ

На Рис. 9 изображено: вверху (над чертой) - известная нам из предыдущей задачи 2 схема производства одного изделия, а внизу (под чертой) - ситуация, когда Изобретатель устранил узкое место в этом процессе. Причём без всякого ущерба для изделия.

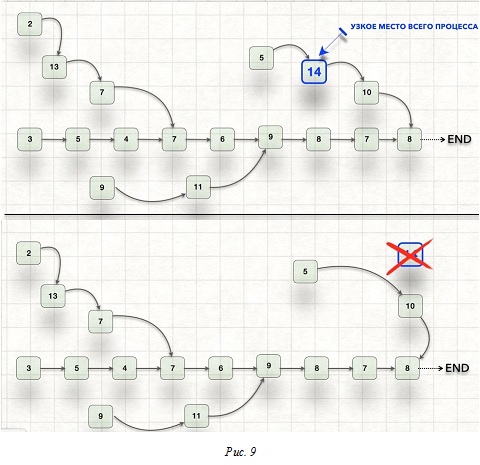
Теперь долгой операции, длившейся 14 минут, нет и даже функция её не нужна.

Ранее (верхняя картинка) за 8-мичасовую смену производили иногда 32, иногда 33 изделия. Вы уже можете сами легко посчитать это значение.

Вопрос первый: "Сколько изделий производят теперь (нижняя картинка, Рис. 9) за ту же 8-мичасовую смену?"

Опция "расшить узкое место" стоит в прайсах многих изобретательских фирм и независимых изобретателей.

Автор этой книги большую часть своей жизни посвятил ТРИЗ (Теории Решения Изобретательских Задач), вследствие чего знаком со многими очень квалифицированными изобретателями (да и сам хорошо владеет этим предметом) и может утверждать без лукавства: практически каждый из таких специалистов не подвергнет сомнению ценность нижней части рисунка 9. Каждый из них будет говорить о "повышении идеальности", будет мотивирован достижением такого результата и будет рад получить заказ на достижение подобной цели.

Более того, можно не сомневаться в том, что будут, хотя бы мысленно, совершены попытки правую верхнюю "ветку" процесса (да и не только её) "свернуть полностью" без ущерба для изделия. Сомнений в экономичности достигнутого результата у того, кто будет думать над этим, не возникнет.

Но всё же давайте ответим на заданный вопрос: "Сколько будет производиться тех же изделий после устранения узкого места?"

Посчитаем. Это значит - найдём n в следующем уравнении: 67 + 13(n - 1) = 480, где 480 минут - нетто-продолжительность смены (8 часов * 60 минут), 67 - время изготовления первого изделия, 13 - продолжительность самой долгой операции усовершенствованного процесса. Итак, n = 32,8 - то есть "иногда 32, иногда 33", то есть ровно столько, сколько и было. Весь "креатив" ушёл на "обогрев Вселенной".

Конечно, для самоуспокоения всегда можно сказать, что "зато сэкономили может даже 1 станок и может даже 1 человека, и заметное количество "незавершёнки" в буфере узкого места", но, очевидно, это совсем не тот результат, которого ожидали от Изобретения.

Между тем несложно было бы предсказать это фиаско прежде, чем отдавать соответствующее поручение. Достаточно посчитать по одной и той же формуле пределы производства при благоприятных условиях в верхней и нижней частях рисунка 9 и сравнить полученные значения.

А теперь вопрос-2:"Предположим, перед Вами поставили задачу заметно, например вдвое, повысить эффективность этого процесса, какая будет Ваша стратегия?" Подумайте прежде чем читать дальше.

И ЧТО ЖЕ ВЫ НАЗЫВАЕТЕ "ЭФФЕКТИВНОСТЬЮ"?

Это часто спрашивают, прочитав вопрос-2 к задаче 3. Что ж, ответ такой:

• Когда за большой прирост результата мы платим малую цену, то говорим что нашли эффективное решение.
• Можно сказать и наоборот: "Когда, по мере движения, разность между затратами и результатом сокращается, мы движемся эффективно, если не ошиблись в направлении". (Если в этом месте у Вас вновь возникла ассоциация с "наименьшим действием", Вы весьма образованы и Вы правы.)
• Часто ещё эффективностью называют "соотношение результата и затрат", но не всегда одно на другое надо делить. И выражение "выгодно купить дополнительный результат за малую цену" хоть и менее частое, но более информативное.

Но ни одному из определений эффективности не соответствуют две ошибки, часто совершаемые при попытках ответить на вопрос 2.

Ошибка-1: Выбор затратной стратегии последовательного усовершенствования 8-ми разных операций.

Разумеется, это плохой замысел: устранив 14 минутную операцию и не добившись прироста, взяться за устранение следующего "узкого места" - операции, длящейся 13 минут, а затем 11, 10, 9, 9, 8, 8. Ведь если кто в качестве результата решил поднять выработку вдвое, тому надо обратить внимание: в рассматриваемой задаче есть 8 операций, которые длятся дольше 7-ми минут.

Между тем квалифицированные инженеры знают: по правилам ТРИЗ начинать надо с "мини-задачи" - нахождения способа получить дополнительный результат "при минимальных изменениях в системе", малыми усилиями. Да и принцип наименьшего действия, из которого выводимы, возможно, все ключевые физические законы, предписывает рассуждать аналогично.

В следующей главе мы покажем как это сделать в нашем случае.

Ошибка-2: Попытка, образно говоря, построить "вечный двигатель первого рода" - то есть в "закрытой" системе "переложить ресурс иначе" в расчёте на дополнительный результат.

Но дополнительный результат всегда существует за пределами системы, а внутри системы будут изменяться только затраты, как не перекладывай. Делая внутреннюю оптимизацию мы можем сэкономить, но добавленной ценности не получим.

Итак, давайте решим мини-задачу...

ПРОДОЛЖЕНИЕ МОЖНО ЗАКАЗАТЬ, ПОСМОТРЕТЬ НА ВЕБИНАРЕ ИЛИ ПОДПИСАТЬСЯ НА ВЕСЬ СЕРИАЛ.

Материал опубликован на сайте "Открытые бизнес-методики и технологии TRIZ-RI" 28 сентября 2020 г.